Etichetă: conditia ca un triunghi sa fie echilateral

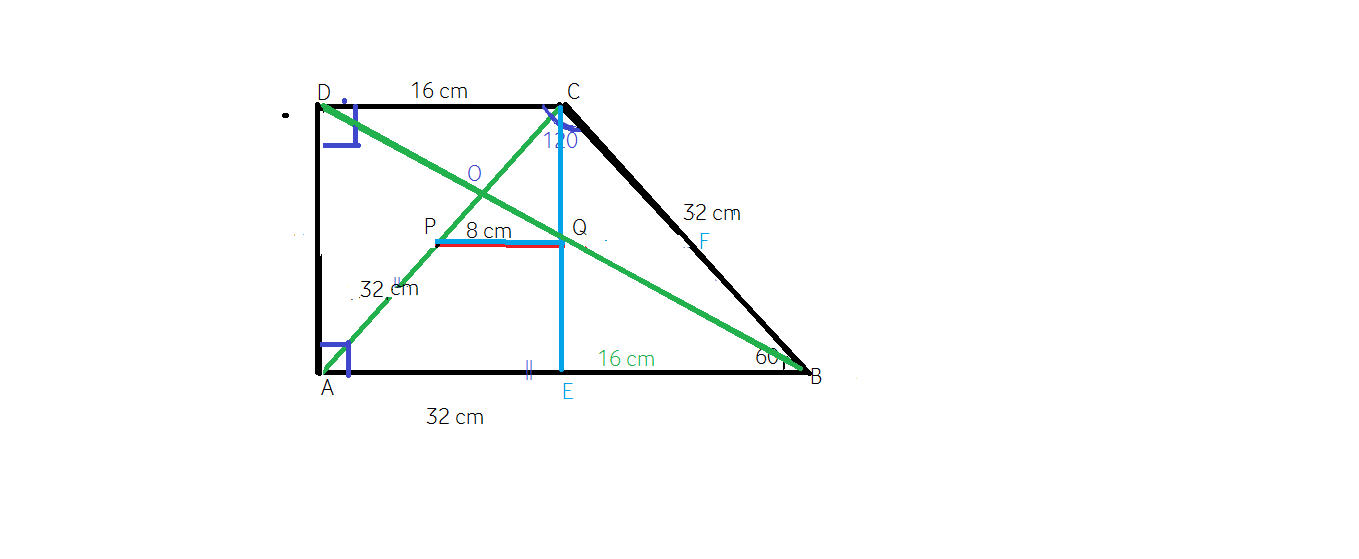
Linia mijlocie intr-un trapez

Dupa ce am discutat despre Linia mijlocie intr-un triunghi a…

Vezi articol…: Linia mijlocie intr-un trapez
Plane perpendiculare

Dupa ce am invatat cand doua drepte sunt perpendiculare acum…

Vezi articol…: Plane perpendiculare