Problema rezolvata cu Teorema celor trei perpendiculare cand baza este Patratul

Enunt problema

Pe planul patratului ABCD de latura $AB = 24\;\;cm$ se ridica perpendiculara $MO\perp\left(ABC\right), MC = 12\sqrt{3}\;\; cm$ , unde O este centrul
patratului. Calculati distantele de la punctul M la laturile patratului.

Demonstratie:

Ipoteza

ABCD patrat

$MO\perp\left(ABC\right) \\MC=12\sqrt{3} cm$

$AC\cap BD=\left\{O\right\}$

Concluzie

$d\left(M, AB\right)=? \\d\left(M, BC\right)=? \\d\left(M, CD\right)=? \\d\left(M, AD\right)=?$

Demonstratie

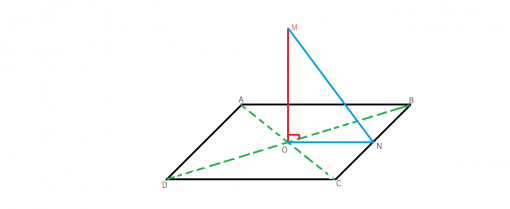
Mai intai realizam figura si scriem toate notiunile pe care le stim:

Stim din ipoteza ca

$MO\perp\left(ABC\right)$

Acum am construit $ON\perp BC, ON, BC\perp\left(ABC\right)\Rightarrow MN\perp BC$

Observati, ca sa aplicam Teorema celor trei perpendiculare trebuie sa formam un triunghi, astfel daca o dreapta este perpendiculara pe un plan, adica $MO\perp \left(ABC\right)$ si prin piciorul ei ducem o dreapta perpendiculara pe o alta dreapta din acel plan, adica $OT\perp BC$ , atunci dreapta care uneste Punctul M cu punctul de intresectie a celor doua drepte este perpendiculara pe cea de-a treia dreapta, adica $MN\perp BC$ .

Deci am aplicat teorema directa a celor trei perpendiculare la aceasta problema rezolvata

Acum ca sa aflam MN, adica distanta de la punctul M la dreapta BC este dreapta MN

$d\left(M, BC\right)=MN$

Cum pe $MO=12\sqrt{3}$ stim din ipoteza problemei, aflam acum ON (ON perpendicular pe BC, deoarece triunghiul OBC este dreptunghic isoscel), astfel stim ca $OC=OB=\frac{l\sqrt{2}}{2}=\frac{24\sqrt{2}}{2}=12\sqrt{2}$ , deoarece stim ca diagonala intr-un patrat este $d_{patrat}=l\sqrt{2}$ , iar ca sa aflam jumatatea diagonalei impartim la doi.

Iar acum ca sa aflam ON aplicam teorema inaltimii, deoarece triunghiul OBC este dreptunghic isoscel, astfel obtinem:

$ON=\frac{c_{1}\cdot c_{2}}{ipotenuza}=\frac{12\sqrt{2}\cdot 12\sqrt{2}}{24}=\frac{144\cdot 2}{24}=\frac{288}{24}=12$ , di ON=12 cm, acum dupa ce am aflat ON aplicam in triunghiul MON Teorema lui Pitagora si obtinem:

$MN^{2}=MO^{2}+ON^{2}\Rightarrow MN^{2}=\left(12\sqrt{3}\right)^{2}+12^{2}\Rightarrow MN^{2}=144\cdot 3+144\Rightarrow MN^{2}=432+144\Rightarrow MN=\sqrt{576}\Rightarrow MN=24\;\; cm$ .

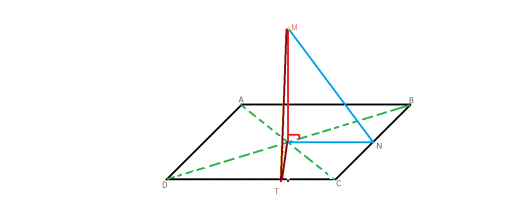
Deci am aflat distanta de la punctul M la dreapta BC, acum ca sa aflam distanta de la punctul M la dreapta AD, dar si distanta de la M la dreapta AB, distanta de la M la dreapta CD observam ca obtinem acelasi lucru adica 24 cm, astfel daca vrem sa aflam distanta de la M la dreapta CD

Astfel stim ca $MO\perp \left(BCD\right)$ , construim

$OT\perp DC$ , stim $OT, DC\subset\left(DBC\right)\Rightarrow MT\perp DC$ , deci $d\left(M, DC\right)=MT$ , acum ca sa aflam MT, stim ca

$DO=OB=OC=12\sqrt{2}$ , cum stim ca triunghiul DOC este isoscel, dar si dreptunghic (acesta rezulta din proprietatile patratului) si astfel putem sa aflam:

$OT=\frac{c_{1}\cdot c_{2}}{ipotenuza}=\frac{12\sqrt{2}\cdot 12\sqrt{2}}{24}=\frac{288}{24}=12 cm$ si astfel daca aplicam Teorema lui Pitagora in triunghiul dreptunghic MOT gasim

$MT^{2}=MO^{2}+OT^{2}\Rightarrow MT^{2}=\left(12\sqrt{3}\right)^{2}+12^{2}\Rightarrow MT=\sqrt{144\cdot 3+144}\Rightarrow MT=\sqrt{576}\Rightarrow MT=24 cm$

Problema rezolvata cu Teorema celor trei perpendiculare cand baza este Patratul

Deci am aplicat teorema directa a celor trei perpendiculare la aceasta problema rezolvata

Recente

Categorii